This is a review of a modern genetic algorithm called multi-offspring improved real-coded genetic algorithm (MOIRCGA). The original paper can be found here. The method used by this algorithm is, formally, called heuristical normal distribution and direction-based crosser (HNDDBX). This algorithm uses generates a direction-based candidate solution and modifies it with some parameterized random variable. The coded algorithm can be found on my github.

Genetic algorithms have been used for optimization since the 1960's. With the increased computational power of modern computers, genetic algorithms have gained attention for solving complex, non-linear objectives. For example, evolutionary strategies are used in neural architecture search, a technique for automating the design of neural networks.

The main use case covered in this paper is constrained optimization. This includes linear programming and non-linear programming optimization problem. Linear programming can be used to find exact solutions for a parameterized function with a set of constraints. However, problems cannot always be defined as a parameterized function. For example, if the problem relying on computing some metric on a large dataset, has a large candidate space, or has fewer constraints than parameters, it might be better to use evolutionary strategies.

MOIRCGA

Formulation Ranking Optimization Components Normal Distribution Crossovers Uniform Distribution Crossovers Combinatorial Mutations Deduplication

Formulation

The code for this example can be found here. A test example for constrained optimization is shown below. The problem has both equality and inequality constraints. Constraints cannot be explicitly applied to genetic algorithms due to the stochastic nature of the algorithm. An L2 penalty can be added to the constraint functions to account for constraints.

The equation below show the original objective function (obj), equality constraint (eq), inequality constraint (ineq), the objective function modified for the gentic algorithm, and the parameters' upper and lower bounds. L2 penalty values, p1 and p2, are applied to the equality and inequality constraints.

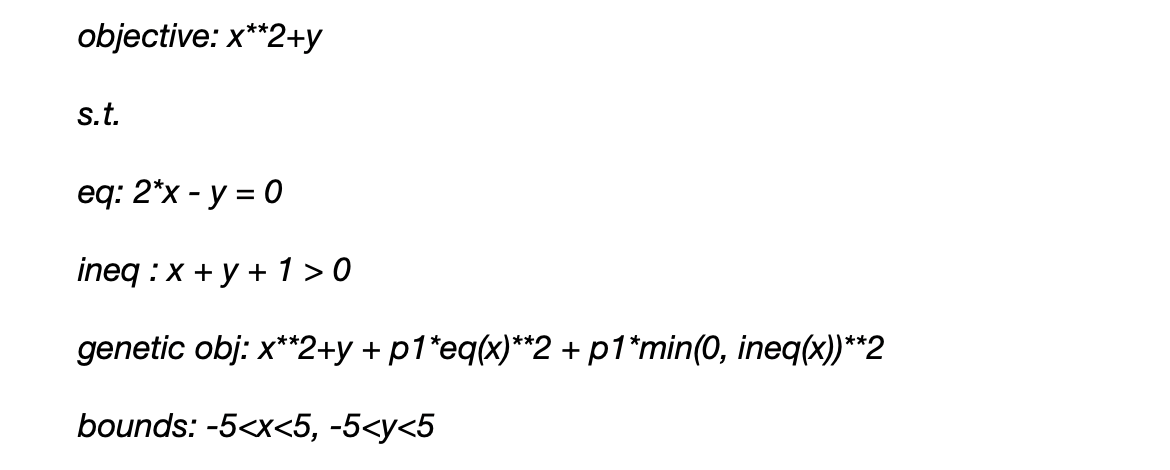
Where eq and ineq are the equality and inequality constraints, respectively. The initial population is generated from a random uniform distribution between the upper and lower bound for each parameter.

Ranking

After the initial population is generated, the losses are calculated for each candidate solution, and the candidates are sorted in ascending order. The population is split into 1…n (top 50th percentile) and n+1…m (bottom 50th percentile). The algorithm will uses these two groups to heuristically calculate the variation or energy of the search space. For example, if there are 100 candidates, the heuristic will use the difference of 1st ranked candidate with the 50th ranked candidate. The algorithm will cycle through each candidate pair and generate new candidate solutions.

Direction Components

The direction components are made of averages between the top candidates. There are four main components: (1) candidate pair XNi (2) candidate pair XMi (3) the average of the top N candidates AVGN (4) the current best candidate BEST (5) an average of (1), (3), and (4) DAVG.

Normal Distribution Crossovers

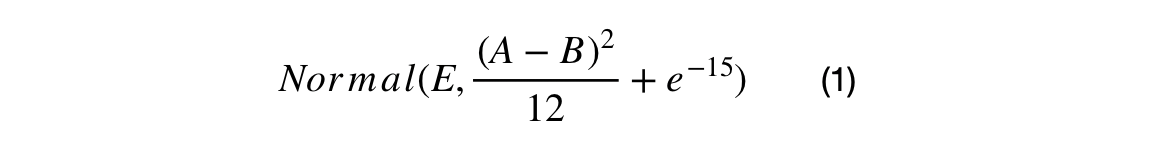
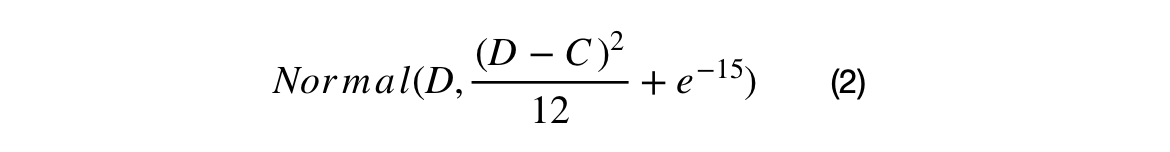
The first crossover searches the space between the AVGN, BEST, and XNi. The search energy is defined as the squared uniform distance between XNi and XMi. The larger the difference between the ith ranked candidate and the 50+ith ranked individual, the larger the search space will be. The second crossover searches around the BEST candidate using the square uniform distance between the BEST and AVGN as the search energy.

Uniform Distribution Crossovers

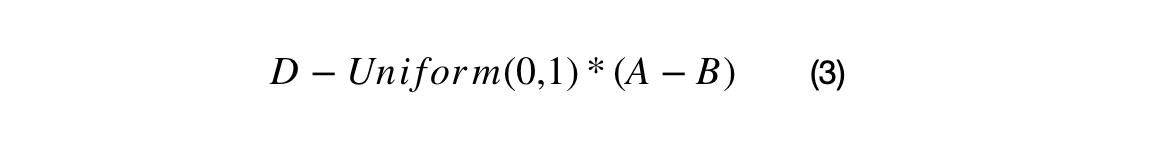
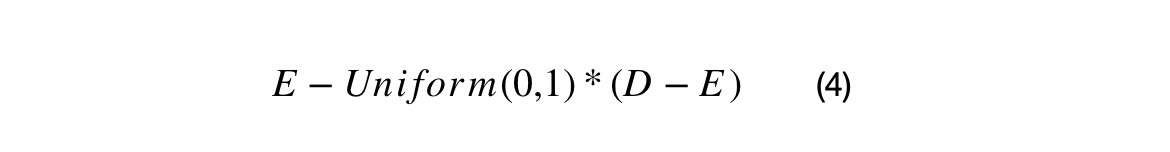
The first crossover uses the difference between XNi and XMi as surrogate gradient. A standard uniform distribution is used with shift the BEST in the direction of the surrogate gradient. The second crossover uses a surrogate gradient with (BEST-DAVG), and it shift DAVG in the direction of the BEST.

Combinatorial Mutations

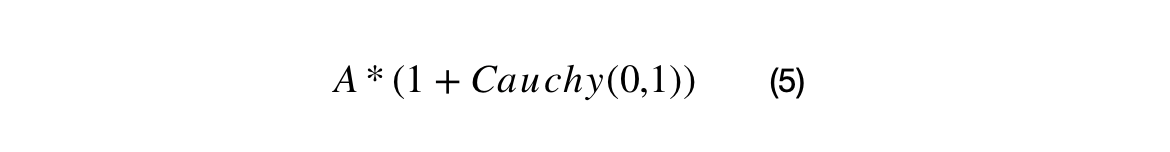
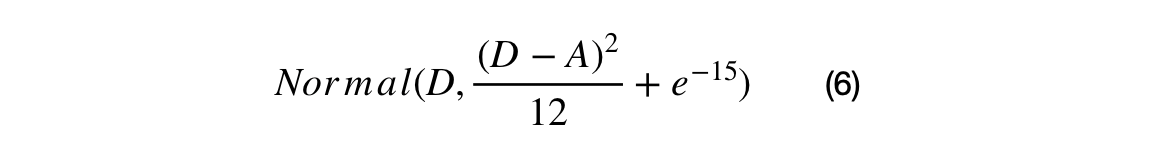
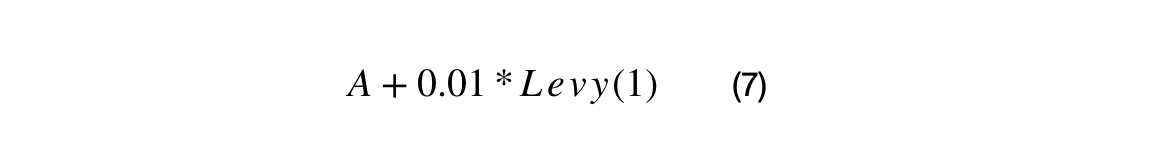
A percentage of the crossover candidates will be mutated by three different operations. The operations can be randomly selected. The standard Cauchy distribution has a median value of 1, but its mean and variance are undefined. The first mutation changes the scale and/or direction of the candidate by some proportion of generated Cauchy number + 1. The second mutation re-samples the candidate around the BEST by the squared uniform distance of BEST to the candidate. The third mutation uses Levy flights to simulate a random walk characterized by many small changes and a few large displacements.

Deduplication

The chance of getting duplicate candidate solutions increased with the number of candidates and convergence to the optimal candidate. In order to keep enough variation in the sample of candidates, the duplicate candidates are removed and replaced with randomly generated candidates.

Recap

The MOIRCGA uses soft margin constraints with various distribution-based search strategies. The direction-based components of the search space are calculated by averaging different top candidates. The energy of the search space is estimated heuristically by the squared uniform distance between various direction-based components. Various mutations are used to effectively search the space around a large space around a candidate. Steps are taken to preserve the variation in the candidate population.